Prime Number Visulization

Prime Number Visualization

Ever wonder what some prime number factoring algorithms look like?

X^2 mod (2^n-1)

In this first set of pictures, I attempted to look at the function x^2 mod (2^n-1). This function is integral to the Lucas-Lehmer (LL) test in Mersenne prime number research. I was hoping there would be a visually recognizable pattern so I could do some optimization. BTW, yes, that's mod (2^n-1), which means you can't simply truncate the upper bits, it's much more complex than that!

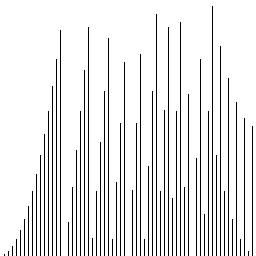
This is the function x^2 mod (2^n-1)

This is the same function, viewed on a log scale

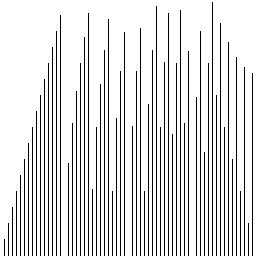
This is the same function with more data points (linear scale)

More Multiplication Optimization

The LL test involves a very large multiplication (typically 10 million binary digits in each factor). If there were some way to reduce the number of operations, it would run much faster. Currently, an FFT Multiply technique (specifically IBDWT-Irrational Base Discrete Weighted Transform) is used. I approached the problem a little bit differently. Instead of using silicon resources for floating point math units, I wanted keep them leaner, and optimize the structure at the bit level.

In this set of pictures, I worked on the assumption that only about 50% of the multiplies need to calculated, since their digits are 0. I wanted to depict what this looks like.

Squaring random numbers: Imagine the white pixels as zeros, and the black pixels as ones. The column on the left is a 2-dimensional representation of the bitwise AND of every digit of a binary number, which is a way of visualizing their product. The column in the middle is the same data, skewed to reflect the proper place value. The final column is the same data, with all-zero rows removed. As you can see, that reduces the multiplication resources by 50%. This isn't anywhere near the optimization level needed to beat front-running implementations of the LL test, but it's very instructive.

Slightly larger numbers.

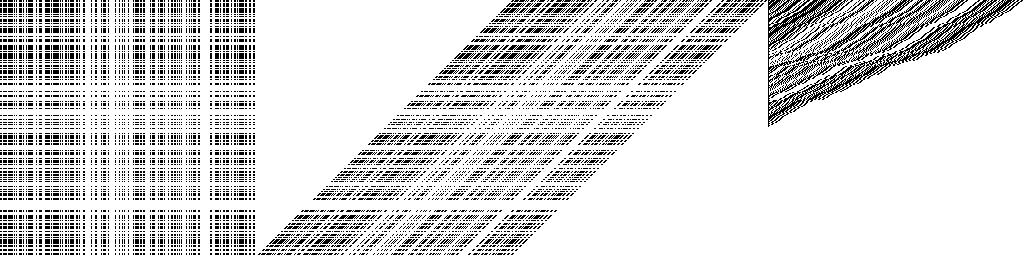
A large number. Notice the detail in the third column. This is our first hint that there's a lot of information in this multiplcation operation, and hence, computational bandwidth.

Choatic Attractor?

In this program, I pondered whether this "operator" X(n+1) = X(n)^2 mod (2^N-1) could be choatic. Perhaps if it was, I reasoned, then some chaos theory science would apply. After all, consider the left shift operator with the MSB wrapping around to the LSB. What it basically means is that the value either doubles with each iteration, and adds 1 in half the cases, or, when the MSB disappears, the delta gets a fixed value subtracted from it while the LSB's double. Got that?

It means a small number doubles and doubles doubles, until it hits a magic range, at which point it begans to come back down toward zero, in an ever-slowing deceleration....until finally, it hits the magic range, and goes back to the top of the slider, where it turns....

Basically, the accumlator suffers from long term impredicability, which is the definition of chaos...So I tried to graph its phase portrait.

An Actual Optimization

I lost many nights of sleep thinking about this stuff, and I actually have something to show for it. I discovered a shortcut you can take when accumulating non-zero rows! What is the optimization? Basically, since your final answer is a modulo value, you need only to add the lowest N LSB's of the delta, and do something special with the MSB by adding its modulus value separately: Since the MSB is either 0, or 2^N, its mod value with (2^N-1) is either 0 or 1 respectively. Therefore, you can simply wrap the MSB of the delta to the LSB. The delta you accumulate is a simple Logical Shift to the left! Imagine the speed this could be implemented in VLSI!

After figuring this out, I wanted to see what it looks like. This is the result of testing 2^13-1 (8191) for primality using the Lucas-Lehmer test with my home-brewed squaring-modulus function:

This is testing 2^19-1. The column on the right is the delta. The column on the left is the accumulator.

This is testing 2^31-1. Notice how the accumlator doesn't change when the row in the right is zero!

This is testing 2^61-1. Notice how we've overblown the standard int size on common machines! I had to implement arbitrary sized integers to do this:

Now, we're getting into the huge numbers: Testing 2^88-1. What's that you say? It's not prime! You're right! Take a look at the very bottom of this picture...Notice how it's still got that 70's pattern. That basically means the final result is non-zero, and it fails the LL test.

Links

Back to Portfolio Noah Vawter
Next Project