Observe that the LSB terms are rather simple, while the MSB terms, since they're the result of much carrying, are more complex. The same observation holds true for many functions of two variables, such as atan2, sqrt(x*x+y*y), etc.
Odd Math
Odd Math is all about replacing those complex, correct logic functions with simplified versions that still give interesting results.
Why? Don't you want accurate math functions? Not always. In fact, in the physical world it's impossible to have perfectly accurate math. Odd Math lets you exchange some accuracy for MASSIVE reductions in cpu time.
I use genetic algorithms to grow the logic equations. They are generally able to execute in a single clock cycle with no pipelining. The accuracy can be surprising. I've gotten as close as 28.5% accurate with a 6-bit multiply so far! The examples below were done with a 44% accurate 7-bit multiplier.
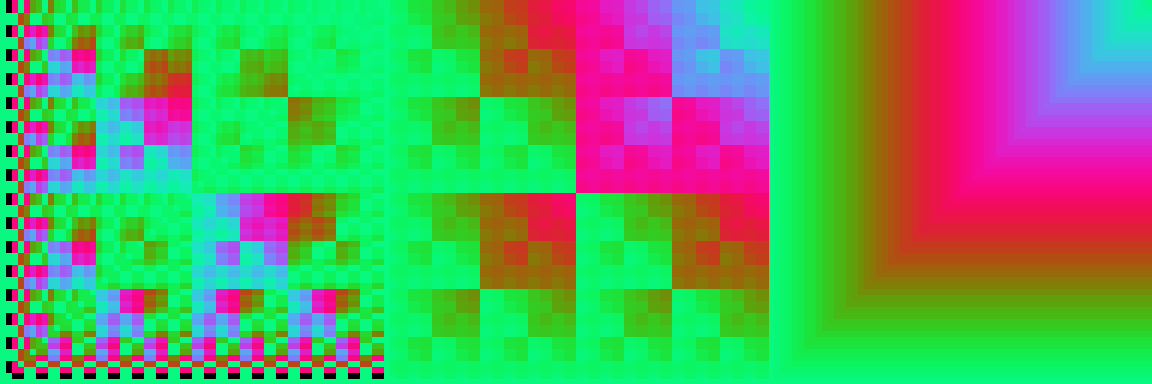
What This Looks Like Graphically
In these graphs, the rightmost section is the target function, the middle section is the generated function, and the left section is the percent error. Black indicates the error is >100%. The target function is is X multiplied by Y. Note: this is normally a symmetric function, but the genetic algorithm found it could gain accuracy by introducing slight assymmetry.Initial (bitwise) estimate of the function:

First generation of genetic algorithm. Notice how much less black area exists in the error graph:
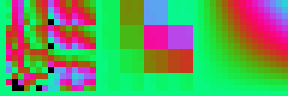
3rd generation. There is now even less black area, and the error is tightened up:
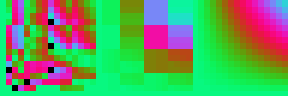
4th generation. No visible changes in this graph, but the error has been reduced even more:
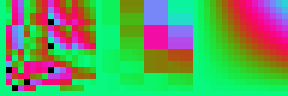
Can I actually hear the effects on audio?
The first half of this project was a 700-line perl program that generated the function approximations. The second half of this project was an implementation the familiar 2-pole svf filter to use my "badmultiply" in place of its normal multiplies. The addition functions were kept pure. A control was added for degree of badness. You can hear the results of various settings on sinusoidal input here:
The samples below are the output of a 2-pole SVF filter sweep on an input signal composed of 4 sinusoids. The sinusoids form a root, fifth, octave, fifth chord. I detune the pitches ever so slightly for a good reason. The chorusing forces the otherwise harmonic waveforms to vary their relative phases, allowing me to more carefully examine the non-linear effects the approximations.